Answer:
D) 2(4+x)=8+2x
Step-by-step explanation:
To be able to determine which of the equations has infinitely many solutions, let's go ahead and solve for x in each of the equations. The equation with infinitely many solutions will have zero on both sides.
1. 5x - 10 = x + 20, to solve for x;

From the solution, x = 5, we can see that this isn't the right option.
2. 2(6+x)=14+2x, let's solve for x;
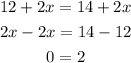
This too isn't the correct option.
3. 10x+5=3(5x+7)
To solve for x;
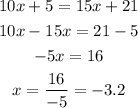
This isn't the correct option too.
4. 2(4+x)=8+2x
Let's solve for x;
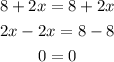
We see from the solution that this is the equation with infinitely many solutions.