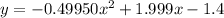Question

How to develop a equation of a parabola given 3 pointsy- intercept : (0, -1.4)x-intercept : (0.905,0)3rd point: (3.07,0.314)

Answer 1

Using the equation:

`y=ax^2+bx+c`

Given the table of values of x and y as shown below:

From the table, when x equals zero, we have y to be -1.4.

Substitute these values of x and y into the above equation.

Thus, we have

`\begin{gathered} y=ax^2+bx+c \\ \Rightarrow-1.4=a(0)^2+b(0)+c \\ \therefore c=-1.4 \end{gathered}`

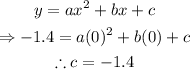
Substitute the obtained value of c into the equation.

This gives

`y=ax^2+bx-1.4\text{ ---- equation 1}`

Also, when x equals 0.905, we have y to be zero.

thus, we similarly substitute the values of x and y into the equation.

`\begin{gathered} y=ax^2+bx+c \\ \Rightarrow0=a(0.905)^2+b(0.905)+c \\ 0=0.819025a+0.905b+c \\ \text{but c=-1.4} \\ \text{thus, we have} \\ 0=0.819025a+0.905b-1.4 \\ \Rightarrow0.819025a+0.905b=1.4\text{ ----- equation 2} \end{gathered}`

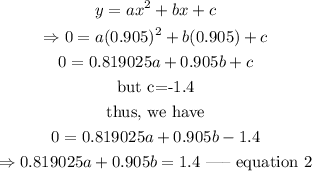
When x equals 2, y equals 0.6. substitiute the values of x and y into the equation.

`\begin{gathered} y=ax^2+bx+c \\ \Rightarrow0.6=4a+2b+\text{c} \\ \text{where c=-1.4} \\ \text{thus,} \\ 0.6=4a+2b-1.4 \\ \text{add 1.4 to both sides of the equation,} \\ 0.6+1.4=4a+2b-1.4+1.4 \\ \Rightarrow4a+2b=2\text{ } \\ \text{divide through by 2 reduces the equation to be} \\ 2a+b=1\text{ ------ equation 3} \end{gathered}`

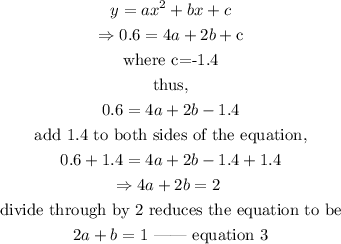
From equation 3, make b the subject of the equation or formula.

Thus,

`\begin{gathered} 2a+b=1 \\ \Rightarrow b=1-2a\text{ ---- equation 4} \end{gathered}`

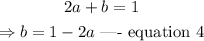
substitute equation 4 intp equation 2.

Thus,

To solve for b, substitute the obtained value of a into equation 4.

From equation 4,

`\begin{gathered} b=1-2a \\ \text{where} \\ a=-0.49950 \\ \text{thus,} \\ b=1-2(-0.49950) \\ \Rightarrow b=1.999 \end{gathered}`

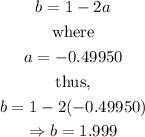
From the obtained values of a, b, and c, equation 1 becomes

`\begin{gathered} y=ax^2+bx-1.4\text{ } \\ \Rightarrow y=-0.49950x^2+1.999x-1.4 \end{gathered}`

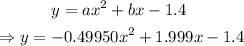
Hence, the equation of the parabola is

`y=-0.49950x^2+1.999x-1.4`