Question

A fet travels 5416 miles against a fetstresm In 8 hours and 6296 miles with the jetstream In the same amount of time.What is the rate of the jet in still air andwhat is the rate of the jetstream?

Answer 1

For the given question:

Let the rate of the jet in still air = x

And the rate of the jetstream = y

At the same time ⇒ rate = distance/time

The jet travels 5416 miles against a jetstream In 8 hours

So,

`\begin{gathered} x-y=(5416)/(8) \\ x-y=677\rightarrow(1) \end{gathered}`

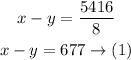
and the jet travels 6296 miles with the jetstream In the same amount of time.

So,

`\begin{gathered} x+y=(6296)/(8) \\ x+y=787\rightarrow(2) \end{gathered}`

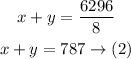
Solving the equations (1) and (2)

So, add the equations to eliminate (y)

`\begin{gathered} 2x=1464 \\ x=(1464)/(2)=732 \end{gathered}`

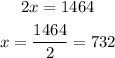
Substitute with (x) into equation (2) to find (y)

`\begin{gathered} 732+y=787 \\ y=787-732=55 \end{gathered}`

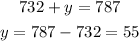
So, the answer will be:

Rate of the jet in still air = 732 mi/hr

Rate of the jetstream = 55 mi/hr