Question

The hexagonal seating section in an auditorium has a small entrance at the front. A walkway leading from the entrance to the front of the stageis 30 ft long. What is the approximate area of the entrance and seating section combined?30 ftft. The area of the entrance isEach side of the hexagon is about ft long. The area of the seating section is aboutabout ft2. The area of the entrance and seating section combines is aboutVv ft²

Answer 1

Given:

Length of walkway = 30 ft

The shape is a hexagon.

A heaxagon is a 6 sided polygon.

Let's solve for the following:

• Length of each side of the hexagon

When we draw two lines from the middle of the walkway to two edges of the hexagon, two right triagles are formed as shown below.

Now, let's find the measure of each angle.

To find the measure, we have:

`(360)/(6)=60`

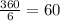
Since the line divides the angle into two parts, the measure of each angle will be:

`(60)/(2)=30^o`

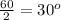
Let's approximate the entrance walkway to be 4 ft.

The adjacent side will be half of the length of the walkway = (30-4)/2 = 26/2 = 13

`\begin{gathered} \tan (30)=(x)/(13) \\ \\ x=13\tan 30 \\ \\ x=7.5 \end{gathered}`

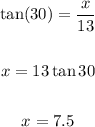
The length of each side will be:

`7.5+7.5=15ft`

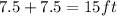
Also, the radius of a hexagon is equivalent to the side length, thus, we have:

side length = 30/2 = 15 ft

Therefore, each side of the hexagon is about 15 ft long.

To find the area of the seating section, we have:

`\begin{gathered} Area=\frac{3\sqrt[]{3}}{2}*15^2 \\ \\ \text{Area}=584.5\approx600ft^2 \end{gathered}`

The area is about 600 square feet.

To find the area of the entrance which forms a rectangle, we have:

Where:

length = 15 ft

width = 4 ft

Area = 15 x 2 = 30 ft²

To find the area of the entrance and seating section, we have:

Area = 600 + 30 = 630 ft².

ANSWER:

• Each side of the hexagon = 15 ft

,

• Area of seating section = 600 ft²

,

• Area of entrance = 30 ft²

,

• Area of entrance and seating section = 630 ft².