Question

Please help me with this question I am trying to help my son to understand this problem better. Solve the system of equations using the linear combination method.{6g+8h=40 −6g+2h=−20}Enter your answers in the boxes.g = _____ h = ___

Answer 1

To answer this question, we need to remember that the linear combination method is a process in which we can add two equations in a way that one of the variables is eliminated, and, therefore, we can solve the equation for the other variable.

In this case, we have:

`\begin{cases}6g+8h=40 \\ -6g+2h=-20\end{cases}`

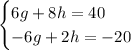
If we add both equations, we have:

`\begin{gathered} \frac{\begin{cases}6g+8h=40 \\ -6g+2h=-20\end{cases}}{0g+10h=20} \\ 10h=20 \\ (10)/(10)h=(20)/(10) \\ h=2 \end{gathered}`

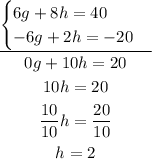
Then we can substitute this value of h in one of the original equations to find g:

`\begin{gathered} 6g+8(2)=40 \\ 6g+16=40 \\ \end{gathered}`

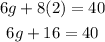
And to solve this equation, we can subtract 16 from both sides of the equation, and then divide both sides by 6:

`\begin{gathered} 6g+16-16=40-16 \\ 6g=24 \\ (6g)/(6)=(24)/(6) \\ g=4 \end{gathered}`

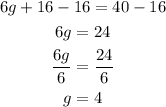
In summary, therefore, we have that the values are:

• g = 4

,

• h = 2