Answer:
2x-5y=-49.
Step-by-step explanation:
Given the line:

Comparing with the slope-intercept form: y=mx+b

Two lines are perpendicular if the product of their slopes is -1.
Let the slope of the new line =n.
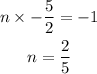
Therefore, the equation of the perpendicular line passing through (-7,7) is:

The equation of the line is 2x-5y=-49.