Question

What is the equation of a line that passes through the origin and intersects (4,6) in slope

Answer 1

By definition, the equation of a line that passes through the Origin, has the following form:

`y=mx`

Where "m" is the slope of the line.

According to the information given in the exercise, the line passes through this point:

`(4,6)`

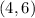
You can identify that:

`\begin{gathered} x=4 \\ y=6 \end{gathered}`

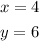
Substituting these coordinates into the equation and solving for "m", you can find the slope of the line. This is:

`\begin{gathered} y=mx \\ 6=m(4) \\ \\ (6)/(4)=m \\ \\ m=(3)/(2) \end{gathered}`

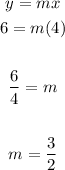
Knowing the slope, you can determine that the equation of this line is:

`y=(3)/(2)x`

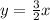
The answer is: Option D.