Step 1
The mid-point of NM is P
Using the mid-point theorem:

We have the coordinates of N and P to be:
N(2,2) , M(3,2)
The coordinates of P is :

Step 2
The mid-point of KL is Q
We have the coordinates of K and L to be:
K(1, 1), L(4, 1)
The coordinates of Q is:
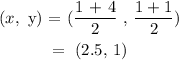
Step 3
The length of PQ can be found using the formula:
![d\text{ = }\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/pg7b3eqvs8y3dq61owmp0ak7y8f3rag9sq.png)
The coordinates of P and Q are (2.5, 2) and (2.5, 1)
Applying the formula, the length of PQ is:
![\begin{gathered} PQ\text{ = }\sqrt[]{(2.5-2.5)^2+(1-2)^2} \\ =\text{ }\sqrt[]{1} \\ =\text{ 1} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wczk4co8tdbipvn9pzwz8nojebmlu2hve8.png)
Answer:
Length of PQ = 1