1 Answer

PaoloFCantoni · Answer 1 · 2023-10-08T05:53:04+0000

The perimeter of the given rectangle is:

$(2x+2*30)\operatorname{cm}=2x\text{ cm+60 cm.}$

Since the perimeter must be equal to or smaller than 70 cm we can set the following inequality:

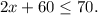
$2x+60\leq70.$

Solving the above inequality for x, we get:

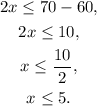
$\begin{gathered} 2x\le70-60, \\ 2x\le10, \\ x\le(10)/(2), \\ x\le5. \end{gathered}$

Answer: Recall that x must be greater than zero since it is the length of the side of the rectangle, then

[tex]0

Please log in or register to add a comment.