The velocity is given by the expression:
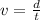
where d is the distance and t is the time.
Plugging the values of the velocity and the distance we have:
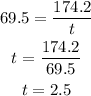
This means that it takes 2.5 hours to reach Seattle; this is the same as 2 hours 30 minutes. Adding this to the hour he left we have that:

This means that Eddie reaches Seattle at 2:05 pm