Here we have that the biggest angle AOD can be written as sums of different angles:
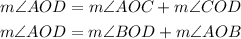
The transitive property of the equality says that if:
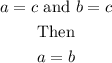
In our case we have:

So according to the property:
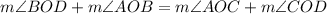
And if:
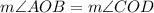
Then we have that:
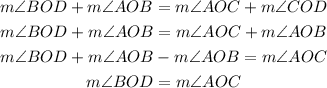
This means that you can prove the statement "if mAOB=mCOD then mBOD=mAOC" by using the transitive property of the equality. Therefore, the correct option is D.