Question

9. A Ferris wheel makes 1 revolution per minute. The linear speed of the seats on the rim of the wheel is 2.14 mph. To the nearest foot, find the radius of the Ferris wheel.

Answer 1

Given:

A Ferris wheel makes 1 revolution per minute, n = 1 rpm

so, the angular speed :

`\omega=(2\pi\cdot n)/(60)=(2\pi\cdot1)/(60)=(\pi)/(30)`

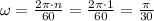
The linear speed of the seats on the rim of the wheel is 2.14 mph

so,

`\begin{gathered} v=\omega\cdot r \\ \end{gathered}`

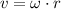
convert from mph to ft/sec

hour = 3600 sec

mile = 5280 ft

so,

`2.14(mile)/(hour)=2.14\cdot(5280)/(3600)(ft)/(\sec)=(1177)/(375)(ft)/(\sec )`

so,

`\begin{gathered} (1177)/(375)=(\pi)/(30)\cdot r \\ \\ r=(30\cdot1177)/(375\pi)=29.97 \end{gathered}`

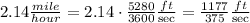
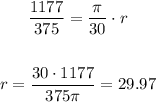
So, the answer To the nearest foot is r = 30 ft