Question

Ryan has an exterminator visit regularly to control an ongoing cockroach problem. It's been working, and the population has declined by 10% every year. If the population is currently 1,245 cockroaches, how many will there be in 3 years?If necessary, round your answer to the nearest whole number.

Answer 1

Since the population declines by 10% each year, then, the population on a given year is 90% of the population of the previous year.

Starting with a population of 1,245 cockroaches, calculate what is 90% of 1,245 to find the population after 1 year by multiplying 1,245 times 90/100:

`1,245*(90)/(100)=1120.5`

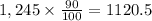
Next, calculate what is 90% of 1120.5 to find the population after two years:

`1120.5*(90)/(100)=1008.45`

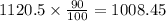
Finally, calculate what is 90% of 1008.45 to find the population after three years:

`1008.45*(90)/(100)=907.605`

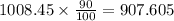
To the nearest whole number, there will be 908 cockroaches after three years.

Notice that another way to find the answer is to multiply 1,245 times (90/100)^3:

`1245*\mleft((90)/(100)\mright)^3=907.605\approx908`

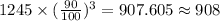
Therefore, the population of cockroaches after 3 years will be 908.