Given the points (5,2) and (10,4), we can find the slope of the line that passes through them with the following formula:

in this case we have the following:
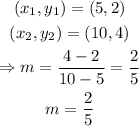
now that we have that the slope is m = 2/5, we can find the equation of the line using the first point and the point-slope formula:
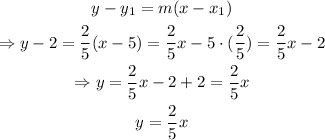
therefore, the equation of the line that contains the points (5,2) and (10,4) is y = 2/5 x