Question

The heights of ten-year-old males are normally distributed with a mean of 57.4 inches and a standard deviation of 5.1 inches. If a pediatrician selects a random sample of 46 ten-year-old males from his patient population, what is the probability that the mean height of this sample will be greater than 57 inches?Round your answer to at least three decimal places

Answer 1

Given:

`Means,\text{ }\mu=57.4`
`Standard\text{ deviation, }\sigma=5.1`
`The\text{ sample size, n=46.}`

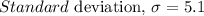
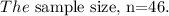
Required:

We need to find the probability that the mean height of this sample will be greater than 57 inches,

`P(x>57).`

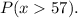
Step-by-step explanation:

Consider the formula to find the z-score.

`z=(\mu-x)/((\sigma)/(√(n)))`
`Subst\text{itue }\mu=57.4\text{, }\sigma=5.1,\text{ n=46 and x=57 in the formula.}`
`z=(57-57.4)/((5.1)/(√(46)))`

`z=(-0.4)/((5.1)/(√(46)))`

`z=-0.4*(√(46))/(5.1)`

`z=-0.5319`

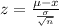
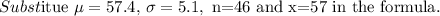
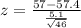
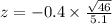
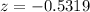
From the z table, we get

`P(x<57)=0.2974`
`\text{We know that }P(x>57)=1-P(x<57).`

`Substitut\text{e }P(x<57)=0.2974\text{ in the equation.}`

`P(x>57)=1-0.2974.`

`P(x>57)=0.7026.`
`P(x>57)=0.703.`

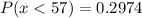
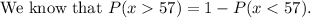
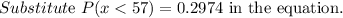
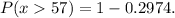
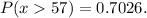
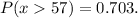
Final answer:

The probability that the mean height of this sample will be greater than 57 inches is 0.703.