Question

An object experiences two velocity vectors in its environment.v1 = −60i + 3jv2 = 4i + 14jWhat is the true speed and direction of the object? Round the speed to the thousandths place and the direction to the nearest degree.

Answer 1

- The object experiences two velocities. We are asked to find the true speed of the object.

- To find the speed of the object, we simply find the resultant of the vectors

- The resultant and direction of the vectors is given as:

`\begin{gathered} R=\sqrt[]{v^2_i+v^2_j} \\ \\ \theta=\tan ^(-1)((v_j)/(v_i)) \end{gathered}`

- Now, let us proceed to solve the question.

- The combination of these velocities is given below:

`\begin{gathered} v_1=-60i+3j \\ v_2=4i+14j \\ \\ V=v_1+v_2=-60i+3j+4i+14j \\ V=-56i+17j \end{gathered}`

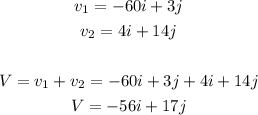
- Thus, we can apply the formulas above:

`\begin{gathered} R=\sqrt[]{(-56)^2+17^2} \\ \\ R=58.5235 \\ \\ \theta=\tan ^(-1)((17)/(-56))=163.113\degree \end{gathered}`

Final Answer

The answer is

58.524, 163° (OPTION 1)