SOLUTION
To answer this question, let us make a diagram for proper illustration
From the diagram above, two alternate angles of 5 degrees and 3 degrees will add up to give us 8 degrees. So the angle facing the side 0.25 miles is 8 degrees
Note that 0.25 miles was gotten thus
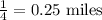
Now, extracting the triangle we need, we have
Now we will find x, using figure a, and then y using the second triangle.
From the first triangle, to find x, we will use the sine rule. From the sine rule,

But the ocean depth under ship A is represented as y in our diagram. So we have to find y. Using the trig-ratio
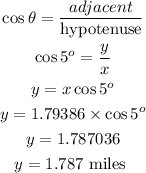
Hence, the answer is 1.787 miles to 3 decimal places