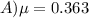
B)It would have skidded 4 times farther.
Step-by-step explanation
the work is the change in energy that results from appliyng a force , in this case, the force is the force of friction
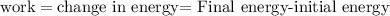
Step 1
find the work done:
Let
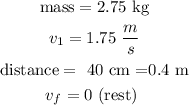
so
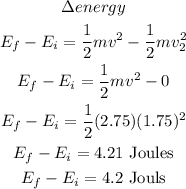
hence, the work and applied force are:

Step 2

now, replace
![\begin{gathered} \mu=(Ff)/(mg) \\ \mu=\frac{10.52}{(2.75\operatorname{kg})(1.75(m)/(s))} \\ \mu=0.363 \end{gathered}]()
therefotre, the cofficient of kinetick friction is 0.363
Step 3
Part B
if the bale of hay had been traveling twice as fast
then let

so
a)
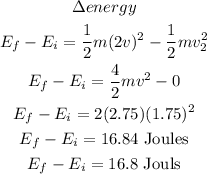
now, replace in the formula
as the force is the same, replace
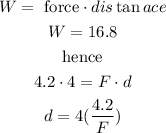
so, we can conclude that
It would have skidded 4 times farther.
I hope this helps you