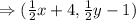The coordinates of the vertices of the original shape are given to be:
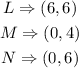
The transformed shape coordinates are given to be:
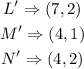
On observation, the shapes show a dilation and a shift in position.
The image has a scale factor of 1/2, meaning it is reduced by 1/2. Therefore, the original coordinates will be reduced to give:
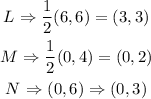
The translation of the initial image can be gotten by subtracting the corresponding coordinates:
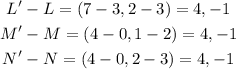
All the differences are the same. This means that the image moves to the right by 4 units and down by 1 unit.
The dilation rule with a scale factor of k is given to be:
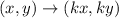
The translation rule for a units to the right and b units down is given to be:
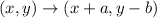
Combining both rules, we have:
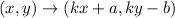
Given:
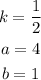
Therefore, the transformation is given to be: