Question

The mean height of women in a certain country ( ages 20 29) is 64.1 inches .A random sample of 70 women in this age group is selected. What is the probability that the mean height for the sample is greater than 65 inches if the standard deviation is 2.52

Answer 1

The mean height is given as 64.1 . We want to obtain the probability that he mean height for the sample is greater than 65 inches ​if the standard deviation is 2.52.

To proceed we, find the z-score of 65 in the distribution, we make use of the formula;

`z=\frac{x-\mu}{(\frac{\sigma}{\sqrt[]{n}})}`

x = 65, mu = population mean = 64.1, sigma = standard deviation = 2.52, n = sample size = 70.

inserting these values, we have;

`\begin{gathered} z=\frac{65-64.1}{\frac{2.52}{\sqrt[]{70}}} \\ z=0.043 \end{gathered}`

The problem now boils down to finding the probability of the z-score greater than 0.043

From z-score tables. the probability of the z-score greater than 0.043;

`Pr(z>0.043)=0.48285`

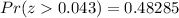
Therefore, the probability that the mean height for the sample is greater than 65 inches is 0.48285