The general slope intercept form equation of a line is as stated below;

where m is the slope and b is the intercept.
If we compare the given equation y = 5x-1 with the equation of a line, we can deduce that the slope, m, is 5.
The slope of a line perpendicular to another is always given as -1/m, therefore the line perpendicular to the line y=5x-1 will have a slope of -1/5;
So let's go ahead and substitute m= -1/5, into the point slope equation to determine the line that passes through (-5,7);
Remember, the point slope form equation of a line is given as;
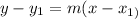
Substituting the above values, we'll have
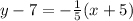
Let's open up the parenthesis first, we'll have;
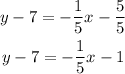
Let's isolate y by adding 7 to both sides of the equation;
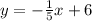
The above equation is the required equation of the line in slope intercept form which can be compared to the one earlier written above(y = mx + b).