Question

An engineer is designing a runway. She knows that a plane, starting at rest, needs to reach a speed of 180mph at take-off. If the plane can reach this take-off speed in 65.0s, how far will the plane travel before take-off. Assume the plane increases speed steadily.

How far does the plane need to travel during take-off (in given units)?
ft
Could the plane take off on a 10000ft long runway?

Answer 1

The plane would need to travel at least
`8,\!580\; {\rm ft}` (
`8.58 * 10^(3)\; {\rm ft}`.)

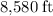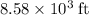The
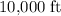`10,\!000\; {\rm ft}` runway should be sufficient.

Step-by-step explanation:

Convert unit of the the take-off velocity of this plane to
`\rm ft\cdot s^(-1)`:

`\begin{aligned}v &= 180\; {\rm mph} \\ &= 180\; {\rm mi \cdot hrs^(-1)} * \frac{1\; {\rm hrs}}{3600\; {\rm s}} * \frac{5280\; {\rm ft}}{1\; {\rm mi}} \\ &= 264\; {\rm ft \cdot s^(-1)}\end{aligned}`.

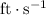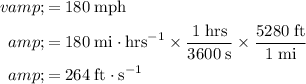Initial velocity of the plane:
`u = 0\; {\rm ft \cdot s^(-1)}`.

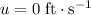Take-off velocity of the plane
`v =264\; {\rm ft\cdot s^(-1)}`.

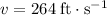Let
`x` denote the distance that the plane travelled along the runway. Since acceleration is constant but unknown, make use of the SUVAT equation
`x = ((u + v) / 2) \, t`.

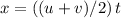Notice that this equation does not require the value of acceleration. Rather, this equation make use of the fact that the distance travelled (under constant acceleration) is equal to duration
`t` times average velocity
`(u + v) / 2`.

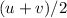The distance that the plane need to cover would be:

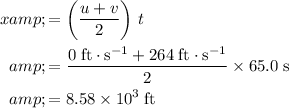`\begin{aligned}x &= \left((u + v)/(2)\right)\, t \\ &= \frac{0\; {\rm ft \cdot s^(-1)} + 264\; {\rm ft \cdot s^(-1)}}{2} * 65.0\; {\rm s} \\ &= 8.58* 10^(3)\; {\rm ft}\end{aligned}`.