Question

Solve the following system. y= 2x^2-3x - 4 and y+ x = 8. Enter the solution with the smaller x value first.

Answer 1

EXPLANATION

Given the system of equations:

(1) y= 2x^2-3x - 4

(2) y + x = 8

Subtract the equations:

y= 2x^2-3x - 4

-

y+x=8

y- (y+x) = 2x^2 -3x-4-8

`\mathrm{Simplify}`
`-x=2x^2-3x-12`
`Switch\text{ sides:}`
`2x^2-3x-12=-x`
`\mathrm{Add\: }x\mathrm{\: to\: both\: sides}`
`2x^2-3x-12+x=-x+x`
`\text{Simplify}`
`2x^2-2x-12=0`

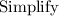
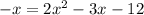
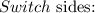
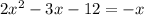
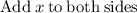
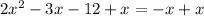
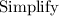
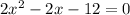
Applying the quadratic formula:

`x_(1,\: 2)=(-b\pm√(b^2-4ac))/(2a)`
`\mathrm{For\: }\quad a=2,\: b=-2,\: c=-12`
`x_(1,\: 2)=(-\left(-2\right)\pm√(\left(-2\right)^2-4\cdot\:2\left(-12\right)))/(2\cdot\:2)`
`x_(1,\: 2)=(-\left(-2\right)\pm\:10)/(2\cdot\:2)`
`Separate\text{ the solutions}`
`x_1=(-\left(-2\right)+10)/(2\cdot\:2),\: x_2=(-\left(-2\right)-10)/(2\cdot\:2)`

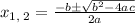
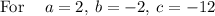
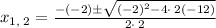
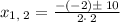
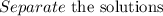
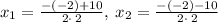
Simplifying:

`x=3,\: x=-2`

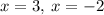
Hence, the solutions are:

x= -2 and x=3

Computing the y-values:

`\mathrm{For\: }y=2x^2-3x-4\mathrm{,\: subsitute\: }x\mathrm{\: with\: }3`
`y=2\cdot\: 3^2-3\cdot\: 3-4`
`y=5`
`\mathrm{For\: }y=2x^2-3x-4\mathrm{,\: subsitute\: }x\mathrm{\: with\: }-2`
`y=2\mleft(-2\mright)^2-3\mleft(-2\mright)-4`
`y=10`

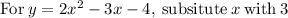
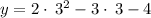
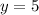
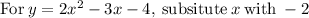
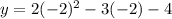
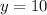
Therefore, the final solutions to the system of equations are:

(x,y) = (-2,10) (x,y)=(3,5)