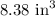Question

Find the volume of the composite solid. FYI: I’m trying to understanding what I’m doing. I just need some clarity on how to get volume of this figure.

Answer 1

Given:

• Radius = 2 in

,

• Height = 2 in

Let's find the volume of the composite figure.

To find the volume of this figure, we are to subtract the volume of hemisphere from the volume of the cylinder.

• Volume of Cylinder:

To find the volume of the cylinder, apply the formula:

`V=\pi r^2h`

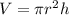
Thus, we have:

`\begin{gathered} V=\pi *2^2*2 \\ \\ V=8\pi\text{ in}^3 \end{gathered}`

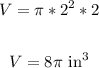
Now, to find the volume of the hemisphere, we have:

`\begin{gathered} V_h=(1)/(2)((4)/(3)\pi r^3) \\ \\ V_h=(1)/(2)*(4)/(3)*\pi *2^3 \\ \\ V_h=(1*4*2^3)/(2*3)\pi \\ \\ V_h=(32)/(6)\pi\text{ in}^3=(16)/(3)\pi\text{ in}^3 \end{gathered}`

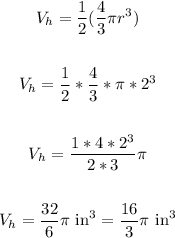
Now, to find the volume of the figure, let's subtract the volume of the hemisphere from the volume of the cylinder.

`\begin{gathered} V=8\pi-(16)/(3)\pi \\ \\ V=(24\pi-16\pi)/(3) \\ \\ V=(8)/(3)\pi\text{ in}^3 \end{gathered}`

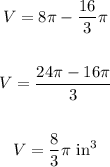
Therefore, the volume of the figure is:

`(8)/(3)\pi\text{ in}^3\approx8.38\text{ in}^3`

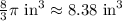
ANSWER:

`8.38\text{ in}^3`