Considering that the dilation factor is 11/6 we have to multiply the sides of triangle ABC to calculate A'B'C'.
When a dilation is happening, you have to multiply the dilation factor times each coordinate of the original triangle.
0. We have to calculate the coordinates of the original triangle:
A(3, 0)
B(3, 6)
C(9, 0)
2. Now, we have to multiply the dilation factor to get the coordinates of A'B'C':
• A'
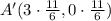
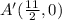
The coordinate of A' is (11/2, 0).
• B'
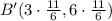
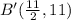
The coordinate of B' is (11/2, 11).
• C'
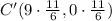
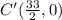
Then, the coordinates of the new triangle are A'(11/2, 0), B'(11/2, 11), and C'(33/2, 0).
Thus, the triangle A'B'C' is:
Then, the lengths of each segment of A'B'C'are:
• C'A' is 11 units.
As we have 0 in the y position, we just have to subtract x position in C' minus x position in A':

• A'B' is also 11 units.
In this case, we consider the position in y and the x position in the same.
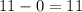
Finally, as it is a right triangle we can use the Pythagorean Theorem to solve this triangle, were
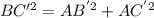
Replacing the values:
![BC^(\prime)=\sqrt[]{11^2+11^2}](https://img.qammunity.org/2023/formulas/mathematics/college/9z4ynj7h7y77226xq0asy9rn6kk8wr272j.png)
Simplifying and solving:
![BC^(\prime)=\sqrt[]{11^2+11^2}\approx15.556](https://img.qammunity.org/2023/formulas/mathematics/college/4wdir6t35dzdgj6bo72uwaii1g5nd4njno.png)
Finally, from the graph we can obtain the segments of triangle DEF using the same procedure as above:
• DE = 11
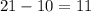
• FD = 11
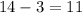
• EF =15.556
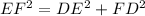
![EF=\sqrt[]{11^2+11^2}\approx15.556](https://img.qammunity.org/2023/formulas/mathematics/college/bimot7xmzmlgt9ftwfe158ktllpeydv324.png)
Then, triangle A'B'C' is equal in sidelength with triangle DEF.
Answer:
• A'(11/2, 0)
,
• B'(11/2, 11)
,
• C'(33/2, 0).
,
• C'A' and DE = 11
,
• A'B' and FD = 11
,
• B'C' and EF = 15.56