Finding how far is an object
We know that:
- The top of the cliff is 40 feet high
- The angle of depression to an object is 32 degrees
We want to find how far is the object from the base, let's call that distance X
We know that
Alternate Interior Angles:
when two parallel lines are crossed by a transversal line the angles of the sides of the transversal are equal
If we simplify the first drawing we have that
Tangent of an angle
We know that
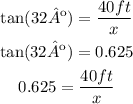
Now we can find x:
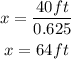
Answer: the object is 64ft far from the base of the cliff