Question

First box: Linear, constant, quadraticSecond box: monomial, trinomial, binomial Third box: 0, 1, 2

Answer 1

Given:

`(3x^2-x-7)-(5x^2-4x-2)+(x+3)(x+2)`

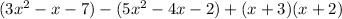
We will simplify the expression as follows:

First, expand the last term which is (x+3)(x+2)

so,

`=(3x^2-x-7)-(5x^2-4x-2)+(x^2+5x+6)`

Second, expand by multiplying the sign in front of each parenthesis

`=3x^2-x-7-5x^2+4x+2+x^2+5x+6`

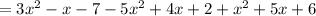
finally, Combine the like terms:

`\begin{gathered} =(3x^2-5x^2+x^2)+(-x+4x+5x)+(-7+2+6) \\ \\ =-x^2+8x+1 \end{gathered}`

So, the result is a quadratic polynomial with 3 terms

So, the answer will be as follows:

First box: Quadratic

Second box: trinomial

Third box: 2