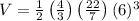The volume of a sphere can be calculated as
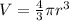
Where r is the radius of the sphere
We want to calculate half of the volume, then we must divide that volume by 2
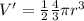
Now we must find the radius of our sphere, the segment AB is the diameter of the sphere, and the radius is half od the diameter, then
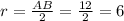
Let's put it into our equation
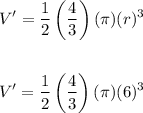
The problem says to use
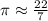
Then
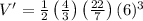
Final answer:
The formula that can be used to calculate the volume of water inside the fish bowl is