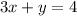Concept: We were told that the point (1,1) is parallel to y = -3x - 1
Let us obtain our slope from the equation given
The general form of equation of line is written in the form
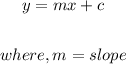
Therefore,

Since, the point is parallel to the line given. Therefore, the slope is the same.
The formula for the equation of the line given one point is,

Thus
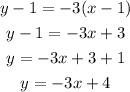
Hence, the equation in its standard form is