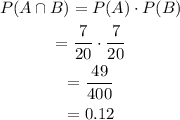Given:
A bag has 1 orange lollipop, 2 red lollipops, 7 Green lollipops, 6 blue lollipops and 4 speckled lollipops.
To find:
The probability of getting a green and then a green.
Step-by-step explanation:
Sample space
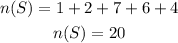
Let A be the event of getting a green lollipop.
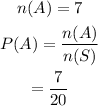
Let B be the event of getting a green lollipop afterpout it back from the first even.
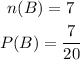
Therefore, The probability of getting a green and then a green is