Question

For the function g(t)=4t^4 -4^t, which of the following statements are true?

Answer 1

D

1) Considering the function, let's find out their Limits:

`\begin{gathered} \lim _(t\to0)\mleft(4t^4-4^t\mright)= \\ 4(0)^4-4^0 \\ 0-(1) \\ -1 \end{gathered}`

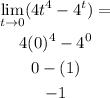
Note that we've plugged into that function, t=0.

2) Now let's check for the 2nd option, following some properties on Limits we have:

`\begin{gathered} \lim _(t\to\infty)(4t^4-4^t)= \\ 4t^4-4^t= \\ \lim _(t\to\infty)(4t^4-4^t)=4(4t^4\mleft(1-(4^t)/(4t^4)\mright)) \\ \\ 4\cdot\lim _(t\to\infty\: )\mleft(t^4\mleft(1-(4^t)/(4t^4)\mright)\mright) \\ \\ \lim _(t\to\infty)(t^4)=\infty \\ \lim _(t\to\infty)(1-(4^t)/(4t^4))=-\infty \\ 4\cdot\infty\cdot\mleft(-\infty\: \mright)=-\infty \end{gathered}`

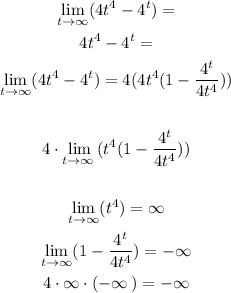
Note that we've used the property of the product of Limits, then calculated each párt of the function separately.

3) And now, let's find out the roots. In a geometric way. Since the roots are the points in which the graph intercepts the y-axis, we have:

Just one root.

Hence, the answer is D