Question

You roll a six-sided die and observe the number showing on the top side when the die comes to rest. What is the probability of observing:a. an even number? b. a number greater than 1? c. a number less than 6? d. a prime number?

Answer 1

`a)(1)/(2)b)(5)/(6)c)(5)/(6)d)(1)/(2)`

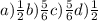
1) Considering that a six-sided dice has all these possible numbers as outcomes we can write our sample space:

`1,2,3,4,5,6`

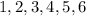
2) So let's calculate the Probabilities:

a) Even number.

Note that we have three even numbers

`1,\mathbf{2},3,\mathbf{4},5,\mathbf{6}`

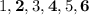
So we can write the Probability of Even numbers as:

`P(\text{even)}=(3)/(6)=(1)/(2)`

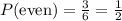
Note that on the denominator, we place the total possible results, and on the numerator the favorable outcomes.

b) A number > 1

Since we've got 5 favorable events (numbers) greater than 1, we can write out:

`P(>1)=(5)/(6)`

c) A number < 6

`P(<6)=(5)/(6)`

Note that similarly to the previous item we have 5 favorable outcomes (1,2,3,4,5) in a total of 6 possible results.

d) A Prime number:

In a six-sided die we have the following prime numbers:

`\mathbf{2},\mathbf{3},4,\mathbf{5},6`

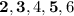
So we have 3 favorable outcomes:

`P(\text{prime)}=(3)/(6)=(1)/(2)`

And that is the answer