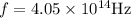Question

What is the frequency (in Hz) of the red light from a laser that has a wavelength of 740.0 nm?answer in:_____ Hz

Answer 1

`f=4.05*10^(14)\text{Hz}`

Step-by-step explanation

Step 1

to solve this we need to use the formula

`\begin{gathered} f=(v)/(\lambda) \\ where\text{ f is the frequency } \\ v\text{ is the wave speed } \\ \lambda\text{ is the wavelength} \end{gathered}`

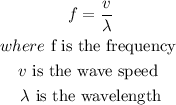
where fis given in Hz, v is m/s and walength in meters

so

a) corvertthe walength fron nm into meters, to do that, divide by 1000000000

`\begin{gathered} 740\text{ nm=}(740)/(10*10^9)m \\ 740\text{ nm=7.4*10}^(-7)m \end{gathered}`

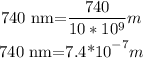
b) then ,let

`\begin{gathered} \lambda=7.4*10^(-7)m \\ speed\text{ }=v=speed\text{ of light=3*10}^8(m)/(s) \end{gathered}`

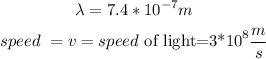
c) finally, replace in the formula

`\begin{gathered} f=(v)/(\lambda) \\ f=(3*10^8(m)/(s))/(7.4*10^(-7)m) \\ f=4.05*10^(14)\text{ Hz} \end{gathered}`

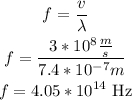
therefore, the answer is

`f=4.05*10^(14)\text{Hz}`

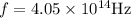
I hope this helps you