The respective graphs are
For material 2:
and for material 3:
We can test each set of functions by substituying a value of x. For instance, when x= 100 we have
Material 1:
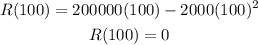
and
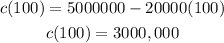
Material 2:
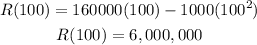
and
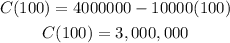
Material 3:
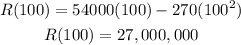
and
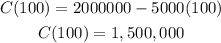
By comparing results, we can see that material 3 can deliver the highest profit about 27,000,000-1,500,000= 25000000.