Given:
The objective is to write cost function for each situation.
Step-by-step explanation:
a)
The fixed charge is, f = $12.
The hourly charge is, h = $1.
Consider the number of hours as x. Then, the cost function can be written as,
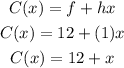
Hence, the cost function is, C(x) = 12+x.
b)
The fixed charge is, f = $445.
The charge per mile is, h = $12.
Consider the number of miles as x. Then, the cost function can be written as,
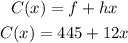
Hence, the cost function is, C(x) = 445+12x.
c)
The fixed charge is, f = 50¢.
The hourly charge is, h = 2(35¢) = 70¢.
Consider the number of hours as x. Then, the cost function can be written as,

Hence, the cost function is, C(x) = 50+70x.
d)
The fixed charge is, f = $44.
The charge per mile is, h = 28¢ = $0.28.
Consider the number of miles as x. Then, the cost function can be written as,
![undefined]()