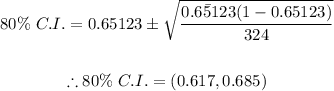Sample size: 324
Number of successes: 211
Confidence level: 80%
The sample proportion of positive results is:
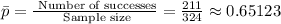
Now, we calculate the significance level α:
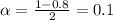
The corresponding z-score is (we look at tables of Z-distribution):
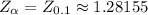
Finally, we apply the formula for the confidence interval (n is the sample size):