The weights of certain machine components are normally distributed with a mean of 8.14 g
Mean = 8.14g
Standard Deviation = 0.09g
The weight that weights that separate the top is express as: P(X>x);
The expression for the normal distribution is express as;

Since, it is given that distribution is 3%
so, P(Z) = 0.03
Substitute the value of Mean = 8.14g , P(Z) = 0.03and Standard Deviation = 0.09g
Now, for the bottom 3%; i.e. Z = 0
From the Z table P(0.03) = - 1.8808
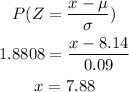
Now, for the distribution that seperate down, is 3%
From the Z table P(0.03) = 1.8808 since, it seperate down
So, P(Z) = - 1.8808

Therefore, the limits that used to identify which components should rejected are 7.88 and 8.31
Answer : 7.88 and 8.31