Given
To find the sine of each acute angle.
Now,
The sine of an angle in a right triangle is given by,
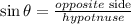
In a right triangle ABC, angle A and angle C are the acute angles, since angle B is 90 degrees (right angle).
Then,
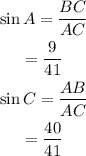
Hence, the sine of each acute angles in the triangle is 9/41 and 40/41.