Given:
The initial horizontal velocity of the projectile, u_x=5.00 m/s
The initial vertical velocity of the projectile, u_y=0 m/s
The height of the cliff, h=10.0 m
To find:
The range of the fight of the projectile.
Step-by-step explanation:
From the equation of motion, the height of the cliff through which the projectile falls during its flight is given by,
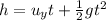
Where g is the acceleration due to gravity and t is the time of flight.
On substituting the known values in the above equation,
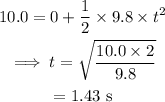
The range of the projectile, that is, the distance between the point where the projectile lands and the base of the cliff is given by,
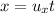
On substituting the known values,

Final answer:
Thus the correct answer is option B.