1 Answer

Jagdish Idhate · Answer 1 · 2023-01-12T02:41:05+0000

Given two points (x₁, y₁) and (x₂, y₂), the slope of the line that passes through these two points can be calculated using the formula:

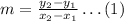
$m=(y_2-y_1)/(x_2-x_1)\ldots(1)$

Using an arbitrary point of the line (x₀, y₀), the slope-point form of the line equation is:

$y-y_0=m(x-x_0)\ldots(2)$

Now, from the problem:

(a)

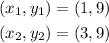
$\begin{gathered} (x_1,y_1)=(1,9) \\ (x_2,y_2)=(3,9) \end{gathered}$

Using (1) to find the slope of the line:

$\begin{gathered} m=(9-9)/(3-1) \\ \Rightarrow m=0 \end{gathered}$

Now, using (1, 9) and (2):

$\begin{gathered} y-9=0(x-1) \\ \Rightarrow y=9 \end{gathered}$

The equation of the line is y = 9

(c)

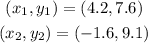
$\begin{gathered} (x_1,y_1)=(4.2,7.6) \\ (x_2,y_2)=(-1.6,9.1) \end{gathered}$

Using (1) to find the slope of the line:

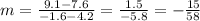
Now, using (4.2, 7.6) and (2):

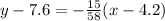
Rounding to two decimal places:

Please log in or register to add a comment.