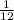Given:
A standard pair of six-sided dice is rolled.
Total number of outcomes is 36.
n(S)=36
To find the probability of rolling a sum greater than or equal to 11:
Here, A= {(5, 6), (6,5), (6, 6)}
So, n(A)=3
Hence, the probability of rolling a sum greater than or equal to 11 is,

Hence, the answer is,