Question

61% of owned dogs in the United States are spayed or neutered. Round your answers to four decimal places. If 36 owned dogs are randomly selected, find the probability thata. Exactly 22 of them are spayed or neutered. b. At most 22 of them are spayed or neutered. c. At least 21 of them are spayed or neutered. d. Between 19 and 27 (including 19 and 27) of them are spayed or neutered. A good calculator is found at: Stattrek Binomial Calculator Round answers to at least 4 decimal places.

Answer 1

Given:

61% of owned dogs in the United States are spayed or neutered.

36 owned dogs are randomly selected,

Required

We need to find the probability.

Step-by-step explanation:

Let n =61% =0.61.

Let p= 36.

We know that mean= np.

Substitute n=36 and p =0.61 in the mean formula.

`Mean=0.61*36`

`Mean=21.96`

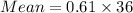
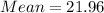
Consider the formula to find the standard deviation.

`SD=np(1-p)`

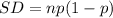
Substitute n=0.61 and p =36 in the formula.

`SD=36*0.61(1-0.61)`

`SD=8.5644`

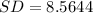
Let x be the number of the spayed dog.

Since np and n(1-p) both exceed 10, we can use the normal distribution.

a)

We need to find the probability of exactly 22 of them being spayed or neutered.

The probability of exactly 22 of them being spayed or neutered is P(x=22).

Consider the z-score value.

`z=(x-mean)/(SD)`

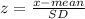
Substitute mean=21.96 and SD=8.5644 in the formula.

`z=(x-21.96)/(8.5644)`
`P(x=22)=P(21.5[tex]P(x=22)=P((21.5-21.96)/(8.5644)<(x-21.96)/(SD)<(22.5-21.96)/(8.5644))`

`P(x=22)=P(-0.0537[tex]P(x=22)=P(z<0.0631)-P(z<-0.0537)`

Use z-table to find the values.

`Use\text{ }P(z<0.0631)=0.5252\text{ and }P(z<-0.0537)=0.4789.`

`P(x=22)=0.5252-0.4789`

`P(x=22)=0.0463`

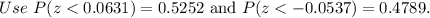
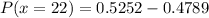
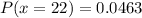
The probability of exactly 22 of them being spayed or neutered is 0.0463.

b)

We need to find the probability of at most 22 of them being spayed or neutered.

`P(x\leq22)=P(x<22.5)`

`P(x\leq22)=P((x-21.96)/(SD)<(22.5-21.96)/(8.5644))`

`P(x\leq22)=P(z<0.0631)`

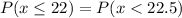
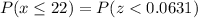
Use z-table to find the values.

`Use\text{ }P(z<0.0631)=0.5252.`

`P(x\leq22)=0.5252.`

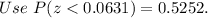
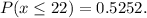
The probability of at most 22 of them being spayed or neutered is 0.5252.

c)

We need to find the probability of at least 21 of them being spayed or neutered.

`P(x\ge21)=P(x>20.5)`

`P(x\ge21)=P((x-21.96)/(SD)>(20.5-21.96)/(8.5644))`

`P(x\ge21)=P(z>-0.1705)`

`P(x\ge21)=1-P(z<-0.1705)`

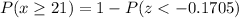
Use z-table values.

`P(x\ge21)=1-0.4323`

`P(x\ge21)=0.5677`

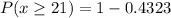
The probability of at least 21 of them being spayed or neutered is 0.5677.

d)

We need to find the probability of between 19 and 27 of them are spayed or neutered.

`P(19\leq x\leq27)=P(18.5[tex]P(19\leq x\leq27)=P((18.5-21.96)/(8.5644)<(x-21.96)/(SD)<(26.5-21.96)/(8.5644))`

`P(19\leq x\leq27)=P(-0.4040[tex]P(19\leq x\leq27)=P(z<0.5301)-P(z<-0.4040)`

Use z table values.

`P(19\leq x\leq27)=0.7020-0.3431`

`P(19\leq x\leq27)=0.3589`

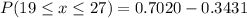
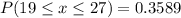
The probability of between 19 and 27 of them being spayed or neutered 0.3589.