Question

I need to know if it’s a, b, c, or D

Answer 1

B. Centre=(-3,-5), Radius=4

Explanation:

Given the circle described by the equation:

`x^2+y^2+6x+10y+18=0`

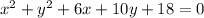
In order to determine the centre and radius of the circle, we write it in the standard form below:

`(x-a)^2+(y-b)^2=r^2\text{ where }\begin{cases}center=(a,b) \\ radius=r\end{cases}`

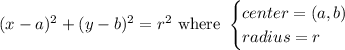
To do this, we use the method of completing the square for both x and y.

Begin by rearranging to bring like variables together.

`x^2+6x+y^2+10y=-18`

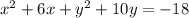
Next, to complete the square in each variable:

• Divide the coefficient of x by 2

,

• Square the result and add to both sides of the equation.

Do the same for y.

`\begin{gathered} x^2+6x+3^2+y^2+10y+5^2=-18+3^2+5^2 \\ \implies(x+3)^2+(y+5)^2=16 \\ \implies(x+3)^2+(y+5)^2=4^2 \end{gathered}`

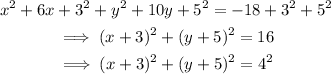
Comparing with the standard form given earlier:

`\begin{gathered} \mleft(x-a\mright)^2+\mleft(y-b\mright)^2=r^2 \\ \mleft(x+3\mright)^2+\mleft(y+5\mright)^2=4^2 \\ \implies a=-3,b=-5,r=4 \\ \text{Centre}=(-3,-5),\text{Radius}=4 \end{gathered}`

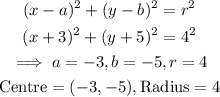
The centre and radius of the circle are (-3,-5) and 4 respectively.