You have this ordered pair:
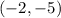
You can identify that its coordinates are:
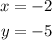
Given the first equation:
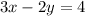
Substitute the value of "x" and the value of "y" into the equation and then evaluate (If the ordered pair is a solution of the System of linear equations, the value on the right side of the equation and the value on the left side must be equal):
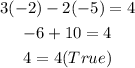
Apply the same procedure in the second equation. Then:
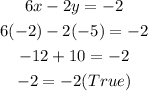
The answer is: The ordered pair is the solution of the System of linear equations.