Question

What is the diameter of the circle whose center is at (6, 0) and that passes through the point (2, -3)?A. 12B. 11C. 5D. 10

Answer 1

We know that the general equation of a circle is

`(x-h)^2+(y-k)^2=r^2`

Where (h, k) is the coordinate of the center of the circle and (x, y) is a point through which the circle passes

In the information of the problem we can see the center and one point

- center: (6, 0)

- point: (2, -3)

So, we must replace the two points in the general equation of a circle to find the radius

`\begin{gathered} (2-6)^2+(-3-0)^2=r^2 \\ (-4)^2+(-3)^2=r^2 \\ 16+9=r^2 \\ 25=r^2 \\ r=\pm\sqrt[]{25}=5\text{ (we take the positive value of the root)} \end{gathered}`

Now, knowing the radius we can get the diameter using the next formula

`\begin{gathered} d=2\cdot r \\ d=2\cdot(5) \\ d=10 \end{gathered}`

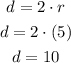
Finally, the diameter is 10 units. Let