Question

You want the volume of the box to be 2 cubic inches.Find the rational solution(s) of the equation. Then use polynomial long division to find the othersolution(s).What are the possible side lengths of the box?

Answer 1

We have a box with cutted corners like in the figure.

The sides of the base of the square are equal to x.

We can calculate the side of the cutted square as (5-x)/2. That will be the height of the box when we fold it.

So, we can express the volume of the box as the product of the area of the base and the height. The area of the base is the product of its sides (x * x).

Then we can write the volume as:

`V=B\cdot h=x^2\cdot((5-x))/(2)=(5x^2)/(2)-(x^3)/(2)`

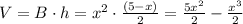
We now have the volume in function of x.

Now, we know that the volume of the box is 2 cubic inches, and we have to find the values of x that make the box be 2 in^3 in volume.

We can write:

`\begin{gathered} V=2 \\ (5x^2)/(2)-(x^3)/(2)=2 \\ (1)/(2)(5x^2-x^3)=2 \\ 5x^2-x^3=2\cdot2 \\ 5x^2-x^3=4 \\ -x^3+5x^2-4=0 \end{gathered}`

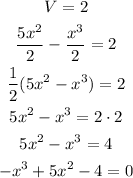
Now, we have to find the roots of this 3rd order polynomial to find the solution.

It is not easy to calculate the roots analitically, but if we do some guessing, we see that x=1 is a solution to the polynomial.

So then, we can divide (polynomial long division) the 3rd grade polynomimal by (x-1) in order to have a 2nd grade polynomial as result:

So we can write the polynomial as:

`-x^3+5x^2-4=(x-1)\cdot(x^2-4x-4)`

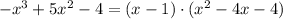
With the quadratic equation, we can calculate the other roots.

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}=\frac{4\pm\sqrt[]{4^2-4\cdot1\cdot(-4)}}{2\cdot1}=\frac{4\pm\sqrt[]{16+16}}{2}=2\pm\frac{4\sqrt[]{2}}{2}=2\pm2\sqrt[]{2} \\ x_1=2+2\sqrt[]{2}\approx4.83 \\ x_2=2-2\sqrt[]{2}\approx-0.83 \end{gathered}`

The only valid solutions are for positive values for x, so the only alternative solution is x=4.83.

The possible side lengths of the box are 1 inch and 4.83 inch.