First, recall that given the equation
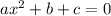
The solutions are given by
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
where the sign in the middle means that we get one root by taking a plus sign and we get the other root by taking a minus sign.
In our case, we have a=1, b=-6 and c=-41. So the solutions of this equation are given by
![x=\frac{-(-6)\pm\sqrt[]{(-6)^2-4(-41)}}{2}=\frac{6\pm\sqrt[]{36+164}}{2}=\frac{6\pm\sqrt[]{200}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/b2bygxd68nf5teco26hm37jf51f65g06ft.png)
Note that
![\sqrt[]{200}=\sqrt[]{100\cdot2}=\sqrt[]{100}\cdot\sqrt[]{2}=10\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/flroyxjbnsemrppsy6zjfdzhrzro4sfqvp.png)
Then
![x=\frac{6\pm10\sqrt[]{2}}{2}=3\pm5\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/d40uc3ltvuqvirgtsdp9pvnq7fsm27tj4x.png)
taking sqrt(2) as 1.4142, we get
![x=3+5\cdot\sqrt[]{2}=10.071\approx10](https://img.qammunity.org/2023/formulas/mathematics/college/d6fujllli9a5di0gnbzkf4j2lgobe57i8m.png)
and
![x=3-5\sqrt[]{2}=-4.071\approx-4](https://img.qammunity.org/2023/formulas/mathematics/college/x1fqvkqvmo0sp7ect053wy12l514hqpe77.png)