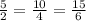From the question, we have the following ratios:
5 : 2, 10 : 4, 15 : 6
Let the diagram velow represent this scenario.
From the figure above we can see that the ratios, 5:2, 10:4, and 15:6 are equivalent, because they increase at a constant rate.
Even though the amounts of each ingredient within a single, double or triple batch are not the same, they would make the fizzy juice that have the same taste.