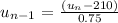See Explanation below
Step-by-step explanation:
a) The given Recursive formula:
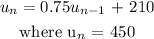
To get u1, n = 1
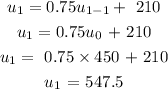
To get u2, n = 2
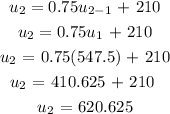
We will follow the above steps to find u3, u4 and u5
b) To find the value of the previous term:
New term = un, previous term = un-1
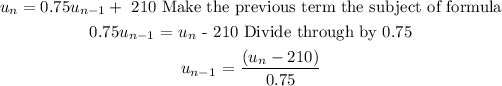
The order of operation is to make the previous term the subject of the formula.
This done by bringing 210 to the other side of the equation: subtract 210 on both sides of the equation.
Then dividing both sides of the equation by the coefficient of the previous equation (0.75).
c) A recursive formula that generates the values from 13a in
reverse order has been derived in question (b)