Question

1. Joe bought a new car in 2011 for $35,000. In 2015, Joe was offered a fair price of $15,000 for his car, but he turned it down.a) Build a linear algebraic model, (i.e., a function), that helps Joe find the car’s value when it is t years old.b) Use your model to give an estimate to the current value of Joe’s car?c) When will the value of the car be zero dollars.

Answer 1

Given data:

The cost price of Joe's car in 2011 = $35, 000

The cost price offered in 2015 = $ 15,000

t is the number of years since 2011.

The general formula for a linear algebraic model is

`\begin{gathered} y=mx+b \\ \text{where,} \\ m=\text{slope} \\ b=y-\text{intercept or initial value} \end{gathered}`

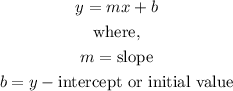
Let y represent the car value's with time

In the year 2011, the value of t = 0

In the year 2015, the value of t = 4, that is (2015 - 2011 = 4)

The coordinates of the data (t, y) are

`\begin{gathered} (t_1,y_1)\to(0,35,000) \\ (t_2,y_2)\to(4,15,000) \end{gathered}`

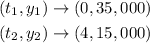
Find the slope (m)

`\begin{gathered} m=(y_2-y_1)/(t_2-t_1) \\ m=(15,000-35,000)/(4-0) \\ m=(-20,000)/(4) \\ m=-5000 \end{gathered}`

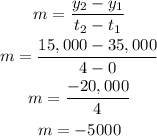
The y-intercept b, that is the initial value is the value of the car (y) when t = 0

`b=35,000`

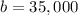
a. Therefore, the linear algebraic model is:

`y=-5000t+35,000`

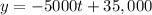
b. Therefore, the current estimated value of Joe's car (that is, in 2021) would be:

`\begin{gathered} y=-5000t+35,000 \\ t=2021-2011=10 \\ y=-5000(10)+35,000 \\ y=-50,000+35,000 \\ y=\text{ -\$}15,000 \end{gathered}`

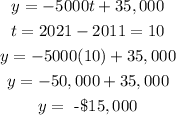
c. The year when the value of the car will be zero dollars will be:

`\begin{gathered} y=-5000t+35,000 \\ 0=-5000t+35,000 \\ 5000t=35000 \\ t=(35000)/(5000) \\ t=7 \end{gathered}`

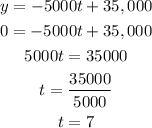
Therefore, after 7 years the value of the car will be zero, the year would be:

`2011+7=2018`

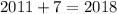
The answers are:

a. The model is y = -5000t + 35000

b. In 2021, the value of Joe's car is -$15,000

c. In the year 2018, the value of the car will be zero dollars